１.  詳細ニューマーク法

【ニューマーク法を整理してみました】の記事で、詳細ニューマーク法という言葉を用いました。

詳細ニューマーク法とは
・地震波形として、動的FEM（等価線形化法などを含め）を用いた応答加速度を用います。
・地震波がどのような地盤を通過してきたかを考慮することが出来ます。
・応答加速度をどのように得るかは解析者によって違います。

一番重要となるのは、動的FEMをやる必要があるという事です。

さて、なぜこのようなことをする必要があるのでしょうか？

場所によって地盤が違うからです。

たとえ同じ地震波であっても、地震波が伝達する地盤が異なれば、応答加速度波形は異なってきます。
対象とする地盤によらず、同じ地震波形を使った解析は（応答加速度倍率にもよりますが）、地震に対する性能を適切に評価できているとは言い難いです。

もちろん、盛土形状や盛土材も場所によって違ってきます。

特に高盛土では、応答加速度倍率（入射波に対する応答値の比率）が高くなる場合がありますので、観測波形そのままを利用するとニューマーク法の変形量を過小評価してしまう事になります。
一方で盛土下部などに軟弱な層が入っている場合には、その限りではありません。
軟弱層によって加速度が減衰してしまいますので、応答加速度倍率が低くなる事もあります。この場合、観測波形を用いるとニューマーク法の変形量を過大評価してしまいます。

これらの地盤の影響を考慮する事ができるのが、詳細ニューマーク法です。

*　地震波が地盤や下図に示すような構造物を通過した場合、その通過した材料の影響を受けます。たとえば、水は方円の器に従うせん断抵抗のない材料です。この場合、当然せん断波(S波)は伝達されません。一方、固体はせん断変形・体積変形をする材料ですから、せん断波(S波)と体積波(P波)の両方が伝達します。伝達時には、地盤の減衰によって加速度振幅が小さくなって伝わることもあります。もちろん、地盤の固有振動数によっては地盤が共振しますので、地震波の加速度振幅が大きくなることがあります。

２.  地震応答解析

地震応答解析（動的FEM）は、運動方程式の時間に関する解き方によって

○運動方程式に対して逐次積分に基づいて解析する方法
（ex. 非線形応答解析）
○運動方程式に対してフーリエ変換を用いて周波数領域で解析する方法
（ex. 等価線形化解析）

があります。
前者は、時間ごとに積分を行っていき、最終的に変位や加速度、応力やひずみを求める手法です。
後者は、フーリエ変換を用いて周波数領域に変換する事で計算するものです。この手法は線形計算用の手法です。

今回は、地盤の繰り返し変形特性を厳密に考慮するために、逐次積分法による非線形動的応答解析（五大開発 SRA-X 利用）を行いました。

下図のようなモデルを考えました。盛土高さ28mの左右対称な盛土になっています。
盛土部をHDモデルとして、その下に線形粘弾性体（レイリー減衰を考慮した弾性体）を用いました。

境界条件は以下のように設定しています。
2E波を用いるため、モデル底面に水平粘性境界条件を用いました。

入力波形は以下を用いました。盛土のないモデルで地表面応答加速度がⅡ-Ⅰ-2（日本道路協会）に近くなるようにgalを調整した波形となります。

*　対象となる地盤を通過して観測波形と似た波形が得られるように調整することは良く行われています。今回は、盛土のない水平成層モデルの地表面でⅡ-Ⅰ-2の波形に近くなるように入力波の最大galを修正しています。この辺りに関しては、また今度ご説明します。

解析メッシュは、以下のように四角形一次要素＋三角形一次要素で構成しました。

材料物性は、以下を用いています。

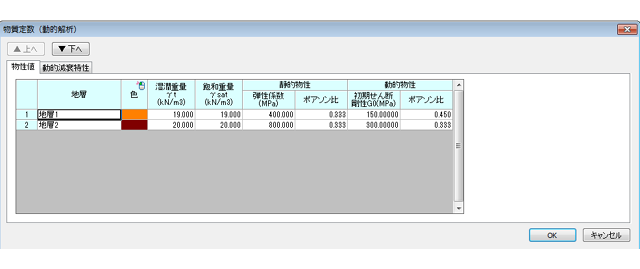
盛土にはHDモデルを用いており、減衰特性を決定する必要があります。
今回はG/G₀-γ、h-γ曲線が下図となるようにHDモデルのパラメータを調整しました。

以上のパラメータを用いて計算した結果を以下に示します。

各要素の偏差ひずみ（一般化工学せん断ひずみ）の時刻歴での最大値をとったものをプロットしたものがこちらになります。

盛土底部中央に大きなひずみが溜まっているのが分かります。ちなみにG/G₀曲線を変化させると（小さなひずみでG/G₀が低くなると……）

このように盛土底部全体に渡ってせん断ひずみが卓越する領域が形成されます。
図を見てわかりますように、偏差ひずみ（一般化工学せん断ひずみ）が10%を超えています。
この場合、剛性は非常に小さくなっていますので応答加速度もかなり減衰してしまいます。
地盤工学会の基準では、両振幅ひずみで5%が液状化と判定されますので、片振幅のひずみが10%というのは、かなり大きなひずみです。

さて、元に返って、最大加速度（絶対値）コンターを見てみますと、綺麗な対称形を描いています。

盛土天端付近がもっとも応答加速度が高く、そこから高さが下がるごとに徐々に応答加速度が低下しています。
逆に言えば、盛土底部から徐々に応答加速度が大きくなるということですから、応答加速度倍率が1以上となり、想定地震波Ⅱ-Ⅰ-2よりも応答加速度波形が大きくなります。

３.  応答加速度

さて、地震応答解析の話は終わって、次はニューマーク法です。
ニューマーク法に関する詳細は、前回・前々回（ ニューマーク法で計算してみました・ニューマーク法で計算してみました その２ ）をご参照願います。

地震応答解析と同じモデルを作り、以下のパラメータを用いた場合の最小降伏震度の円弧が上図となります。

この円弧内の頭部・中部・底部の応答加速度波形を用いてニューマーク法を検討します。
円弧内に含まれるすべての節点の応答加速度の質量平均・算術平均を取る手法があります。
今回は応答加速度の効果が分かり易いように、頭部・中部・底部の応答加速度波形を取得しました。こちらになります。

図を見てわかりますように、底部・中部・頭部と標高が高くなるごとに最大加速度が大きくなっています。

対象としていた元の波形（Ⅱ-Ⅰ-2）はこちらです。
最大galは約760です。各応答波形の最大galは、それぞれ820gal・1000gal・1200galとなっていますので、最大で1.5倍ぐらいgalが違っています。
地盤の影響を考慮する事でこのような結果が得られます。
これが詳細ニューマーク法を行う醍醐味でもあります。

また、参考程度ですが、中部で応力を算出したものがこちらです。
横軸工学せん断ひずみγ、縦軸せん断応力τ_xyです。
今回用いた解析は、逐次積分型の非線形応答解析ですので、HDモデルの骨格曲線/履歴曲線に従って、しっかりヒステリシスを描いて応力が計算されているのがわかります。

ちなみに、先ほど示したG/G₀を変更した場合ですと、

こんな応力分布が得られます。

４.  ニューマーク法

地震応答解析から得られた応答加速度を用いてニューマーク法を行います。
基本的には普通のニューマーク法と手順は変わりません。
ニューマーク法の流れからしますと、用いる地震波形が違うだけになります。

ニューマーク法による計算結果は、以下となります。

上図に示しますように、応答加速度を用いる事で非常に大きな変形が発生しているのが分かります。
このように地盤の特性を考慮した応答加速度を用いると、元々用いようとしていた波形を使った時よりも変形が大きくなることがあります。
特に応答加速度倍率が大きくなる高盛土では、注意が必要です。